Control
the kernel of cybernetics
This page contains fill-in notes on Control: the kernel of cybernetics lectures from the courses ME 370, ME 454, EE/ME 477, MME 554, and MME 577.
Single file
A single pdf with all lectures can be downloaded here.
Individual lecture files
Click the thumbnails on the notes below to get a pdf version.
01.1 Performance
01.2 Feedback control system block diagrams
01.3 Introducing PID control
01.4 An interactive PID controller design
01.5 Exercises for Chapter 01 intro
02.1 Introduction
02.2 Stability from the transfer function
02.3 Routh.Hurwitz criterion
02.4 Exercises for Chapter 02 stab
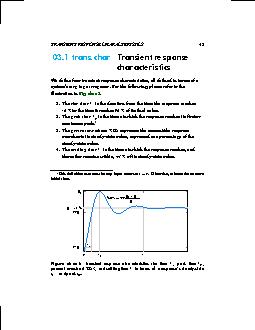
03.1 Transient response characteristics
03.2 Exact analytical trans response char of first. and second.order sys
03.3 Approx analytical transient response characteristics
03.4 Simulation
03.5 Exercises for Chapter 03 trans
04.1 Steady.state error for unity feedback systems
04.2 Exercises for Chapter 04 steady
05.1 Root locus definition
05.2 Sketching the root locus
05.3 Generating the root locus via a computer
05.4 Exercises for Chapter 05 rlocus
06.1 Gain from the root locus
.jpg)
06.2 Proportional controller design (P)
06.3 Beyond proportional design
_controller_design.jpg)
06.4 Proportional.integral (PI) controller design
06.5 Proportional.lag controller design
_controller_design.jpg)
06.6 Proportional.derivative (PD) controller design
06.7 Proportional.lead design
06.8 Prop.integral.derivative controller design
06.9 Proportional.lead.lag controller design
06.10 Multiple derivative compensators
06.11 Exercises for Chapter 06 rldesign
07.1 Introduction
07.2 Bode plots
07.3 Bode plots for simple transfer functions
07.4 Sketching Bode plots
07.5 Nyquist criterion
07.6 Stability from the Nyquist plot
07.7 Stability GM and PM from Bode plots
07.8 Relations among time and frequency domain reps
07.9 Exercises for Chapter 07 freq
08.1 Transient response design by adjusting the gain
08.2 Exercises for Chapter 08 freqd
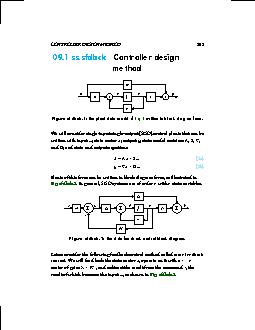
09.1 Controller design method
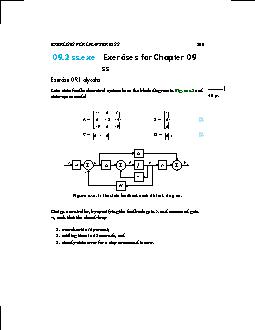
09.2 Exercises for Chapter 09 ss