Measurement
an introduction
- Single file
-
Lecture files
- 01.00 Theoretical foundations
- 01.01 Mathematical measurement theory
- 01.02 Operationalism conventionalism and realism
- 01.03 Information theoretic descriptions of measurement
- 01.04 Model based descriptions of measurement
- 01.05 Epistemology of measurement
- 02.00 Signals
- 02.01 Types of signals
- 02.02 Fourier series
- 02.03 Fourier transforms
- 02.04 Sampling
- 02.05 Nyquist sampling theorem aliasing and reconstruction
- 02.06 Discrete Fourier transforms
- 02.07 Problems for Chapter 02
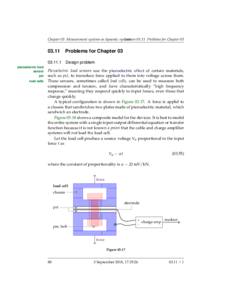
- 03.00 Measurement systems as dynamic systems
- 03.01 Dynamic system representations
- 03.02 Zeroth order measurement systems
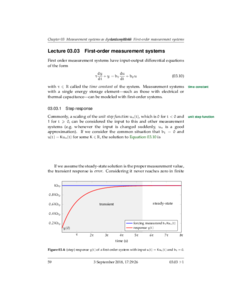
- 03.03 First order measurement systems
- 03.04 Second order measurement systems
- 03.05 Second order measurement systems
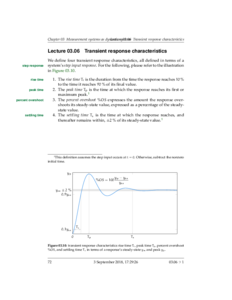
- 03.06 Transient response characteristics
- 03.07 Transient response characteristics
- 03.08 Properties of linear time invariant systems
- 03.09 Response to periodic inputs
- 03.10 Phase linearity
- 03.11 Problems for Chapter 03
- 04.00 Probability statistics and estimation
- 04.01 Probability and measurement
- 04.02 Introduction to set theory
- 04.03 Basic probability theory
- 04.04 Independence and conditional probability
- 04.05 Bayes' theorem
- 04.06 Populations samples and machine learning
- 04.07 Random variables
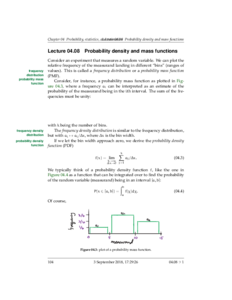
- 04.08 Probability density and mass functions
- 04.09 Expectation
- 04.10 Central moments
- 04.11 Estimation of sample mean and variance
- 04.12 Confidence
- 04.13 Student confidence
- 04.14 Multivariate probability and correlation
- 04.15 Regression
- 05.00 Uncertainty analysis
- 05.01 Design stage uncertainty analysis
- 05.02 Functional propagation of uncertainty
- 05.03 Rigorous uncertainty analysis
- 06.00 Electricity measurement
- 06.01 Instrumentation for electricity measurement
- 06.02 Measuring resistance well
- 07.00 Digital measurement
- 08.00 Temperature measurement
- 09.00 Pressure and velocity measurement
- 10.00 Flow measurement
- 11.00 Strain measurement
- 12.00 Sensors actuators and control
- A.00 Algebra and trigonometry reference
- A.01 Quadratic forms
- A.02 Trigonometry
- B.00 Distribution tables
- B.01 Gaussian distribution table
- C.00 Bibliography
This page contains fill-in notes on Measurement lectures from the course ME 315.
For source code from the lectures, see the source code page.
Single file
A single pdf can be downloaded here.
Lecture files
Click the thumbnails on the notes below to get a pdf version.