Mathematical Foundations of Engineering Analysis
This page contains fill-in notes on Mathematical Foundations of Engineering Analysis lectures from the courses MME 502.
Single file
A single pdf with all lectures can be downloaded here.
Individual lecture files
Click the thumbnails on the notes below to get a pdf version.
1.01 Truth
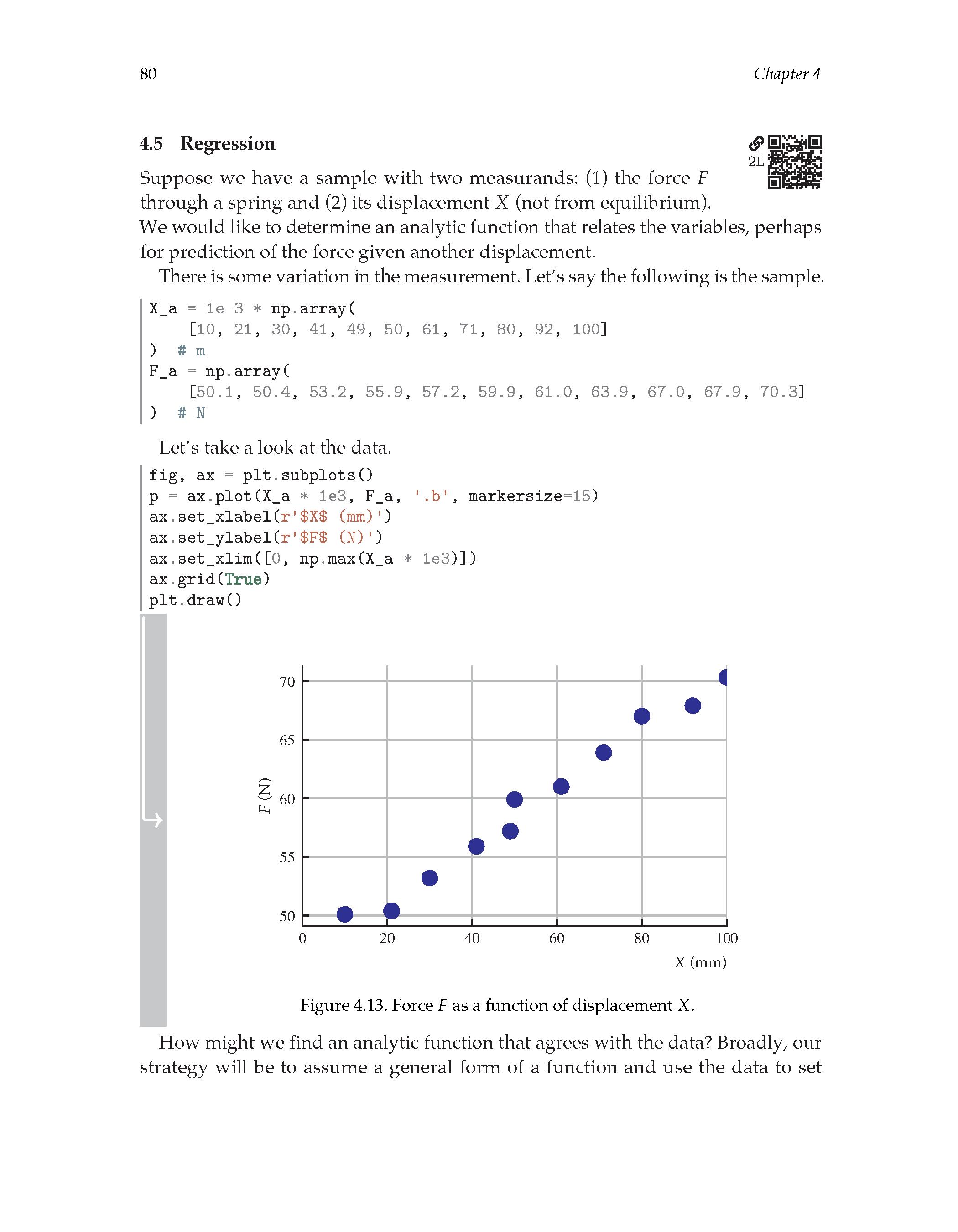
1.02 The foundations of mathematics
1.03 Problems
2.01 Introduction to set theory
2.02 Logical connectives and quantifiers
2.03 Problems
3.01 Probability and measurement
3.02 Basic probability theory
3.03 Independence and conditional probability
3.04 Bayes theorem
3.05 Random variables
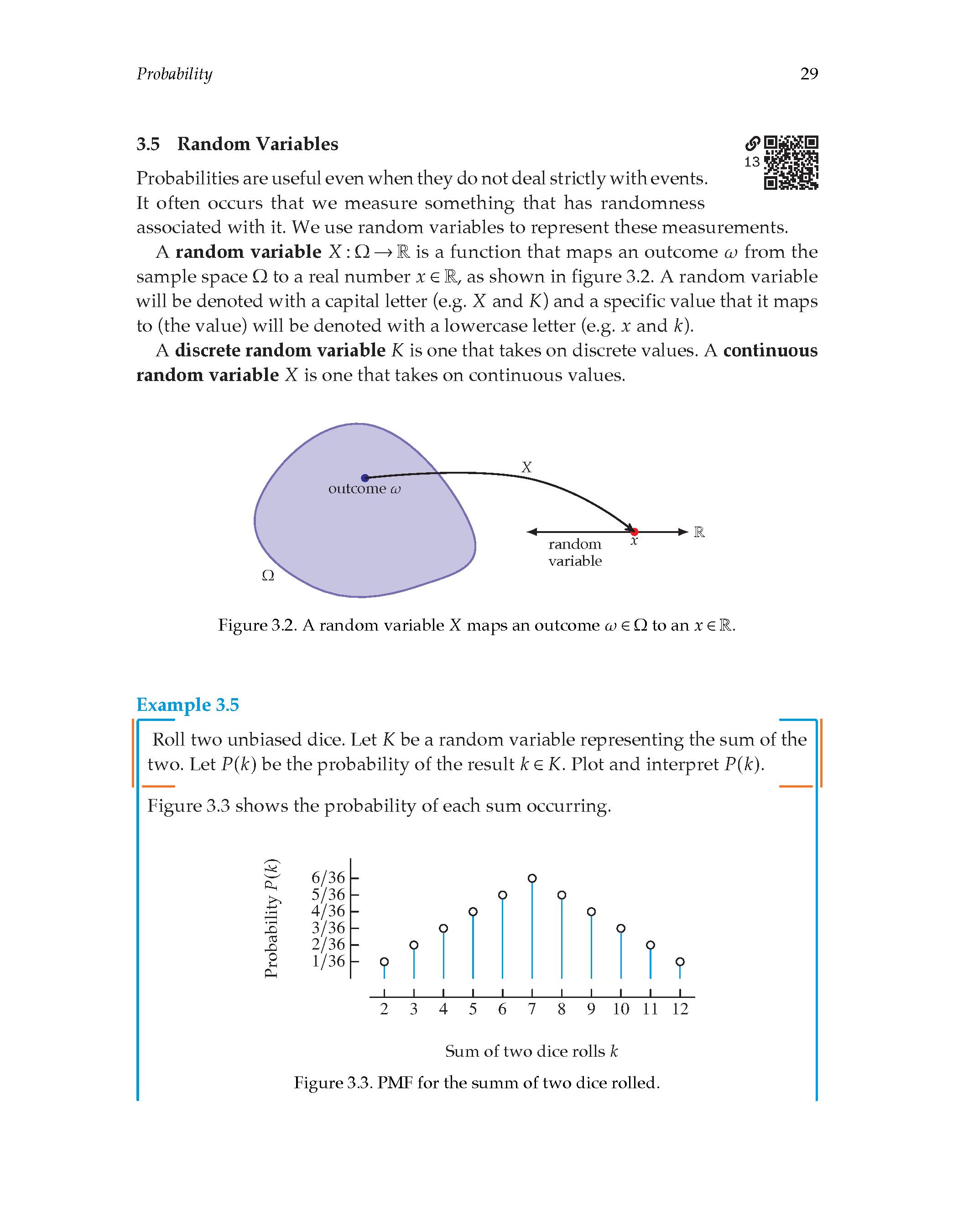
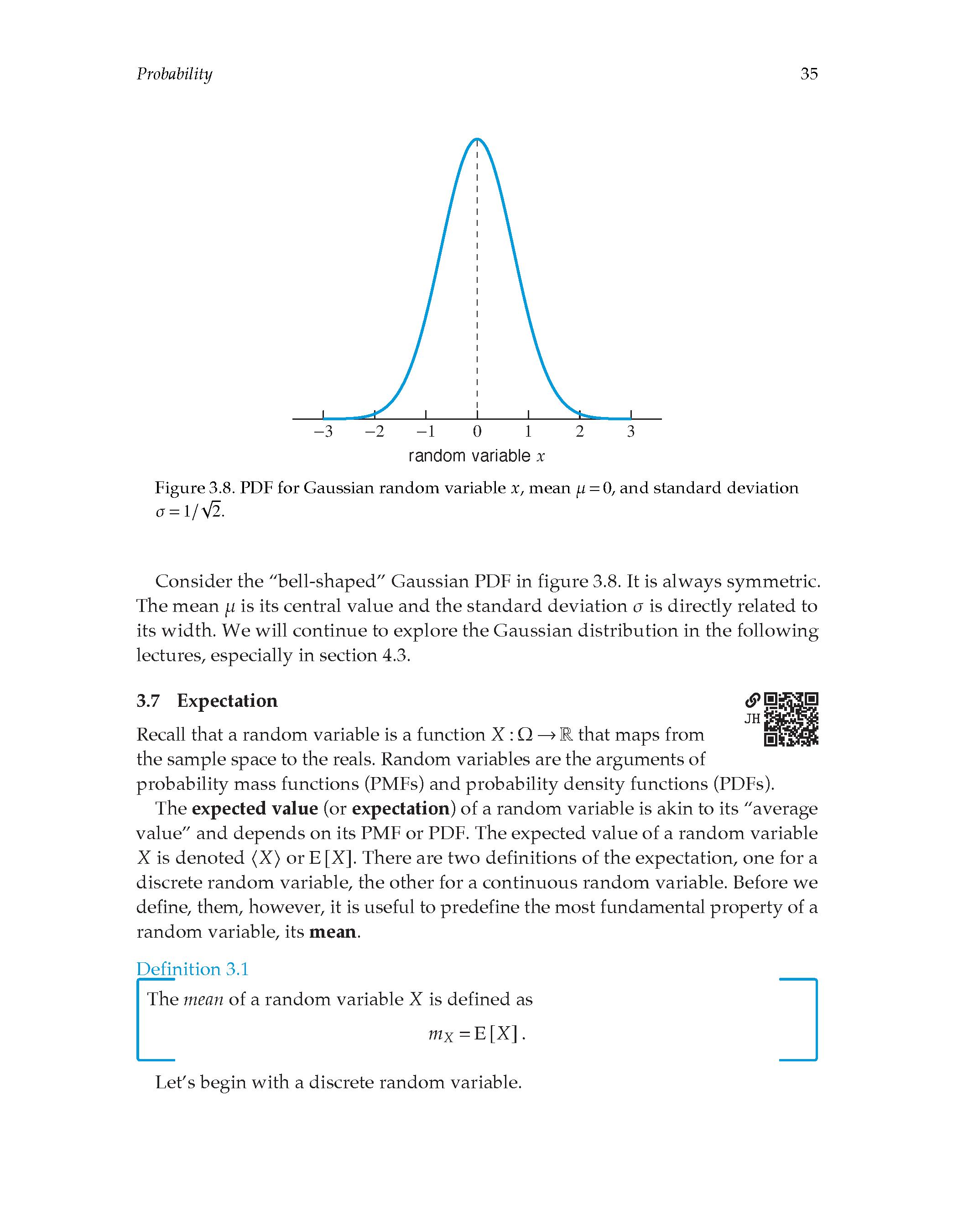
3.06 Probability density and mass functions
3.07 Expectation
3.08 Central moments
3.09 Transforming Random Variables
3.10 Multivariate probability and correlation
3.11 Problems
4.01 Populations samples and machine learning
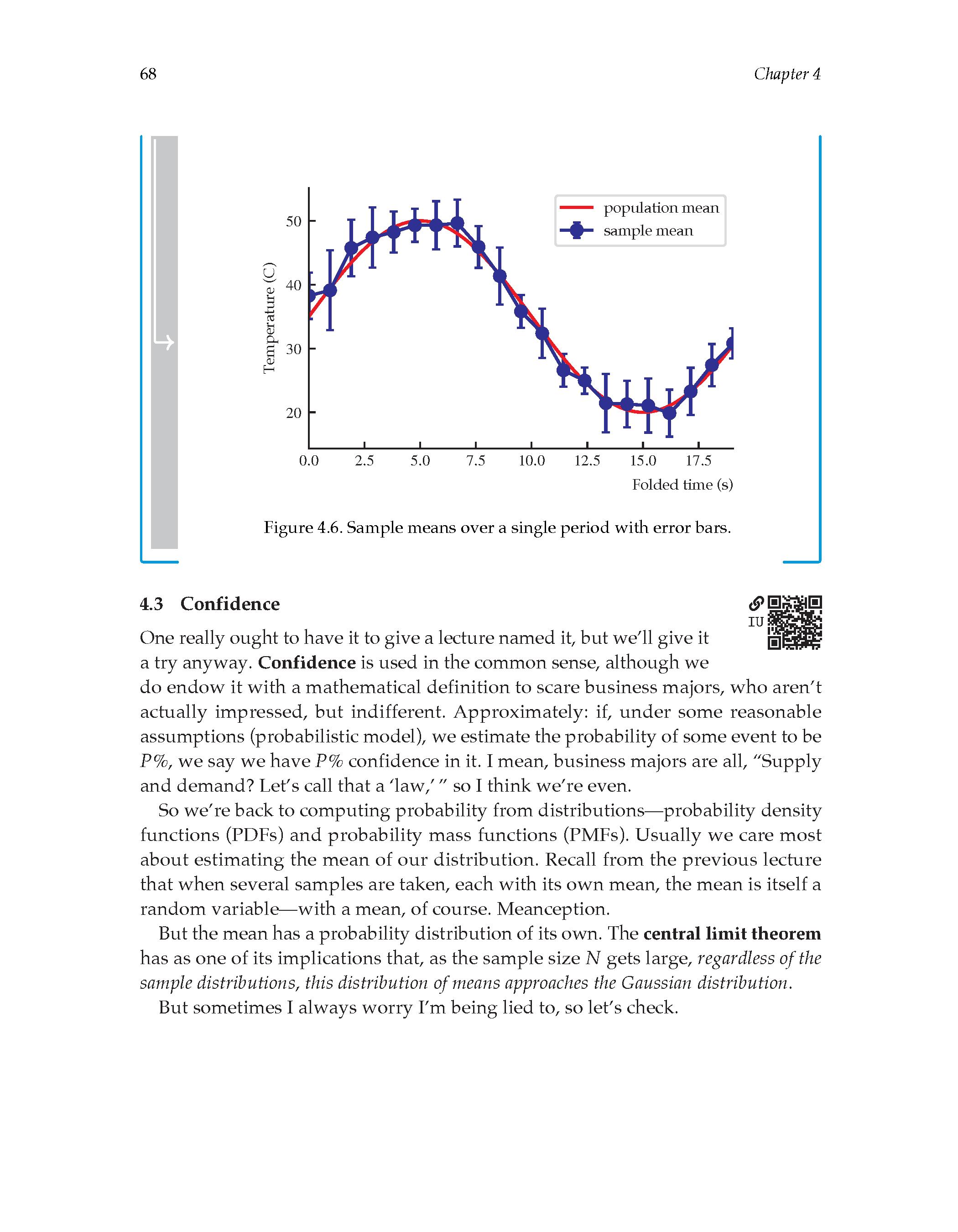
4.02 Estimation of sample mean and variance
4.03 Confidence
4.04 Student confidence
4.05 Regression
4.06 Problems
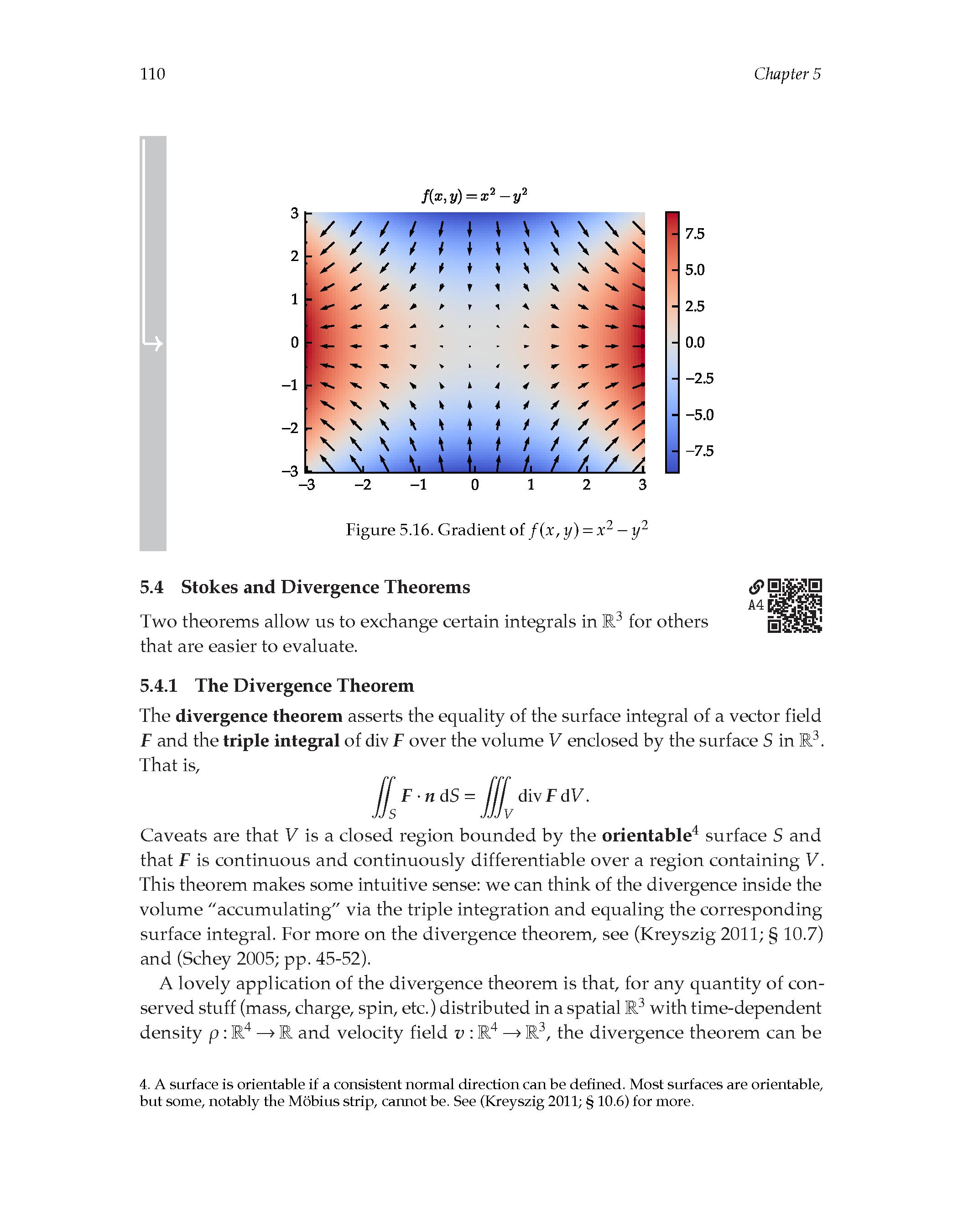
5.01 Divergence surface integrals and flux
5.02 Curl line integrals and circulation
5.03 Gradient
5.04 Stokes and divergence theorems
5.05 Problems
6.01 Fourier series
6.02 Fourier transform
6.03 Generalized fourier series and orthogonality
6.04 Problems
7.01 Classifying PDEs
7.02 Sturm.liouville problems
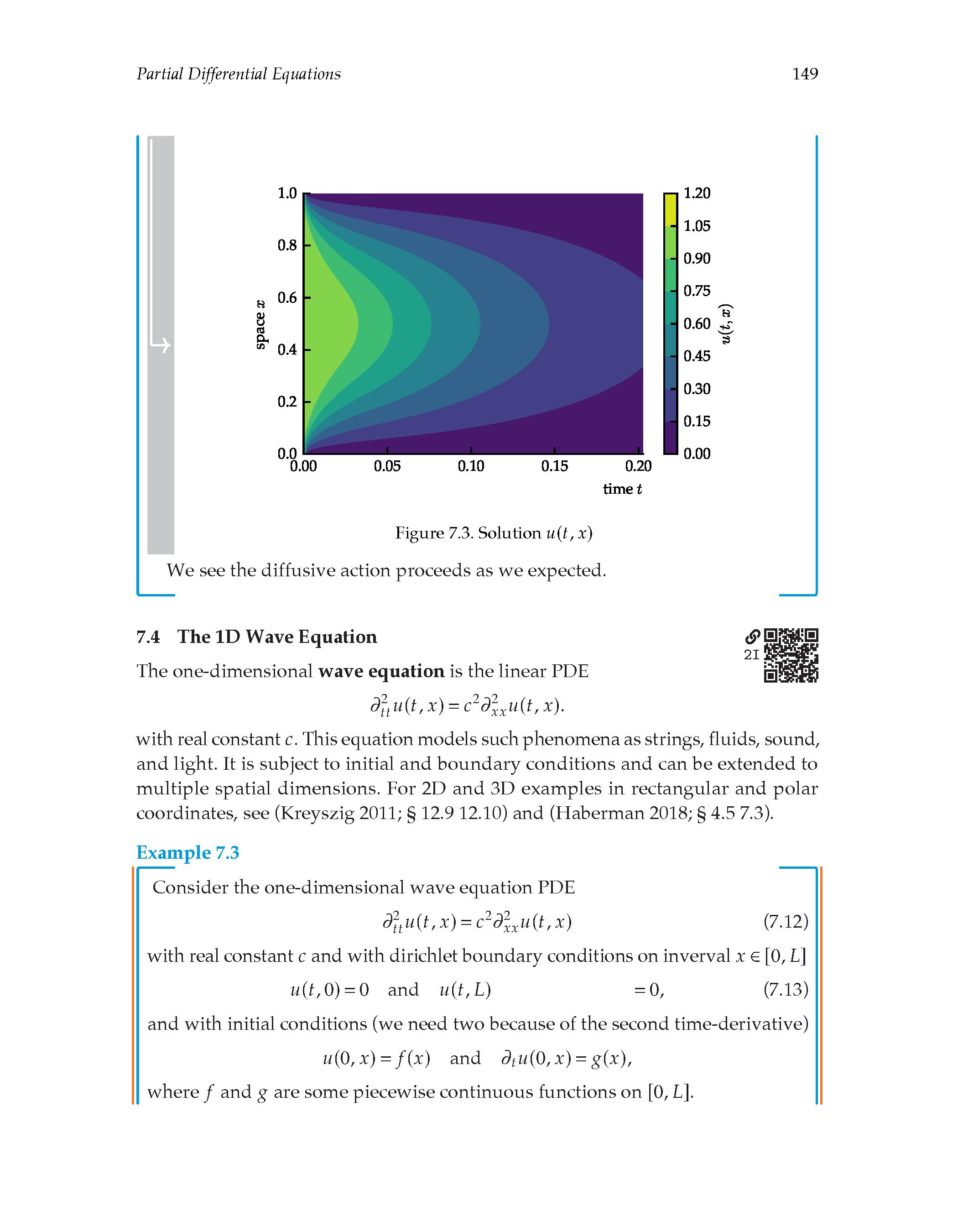
7.03 PDE solution by separation of variables
7.04 The 1D wave equation
7.05 Problems
8.01 Gradient descent
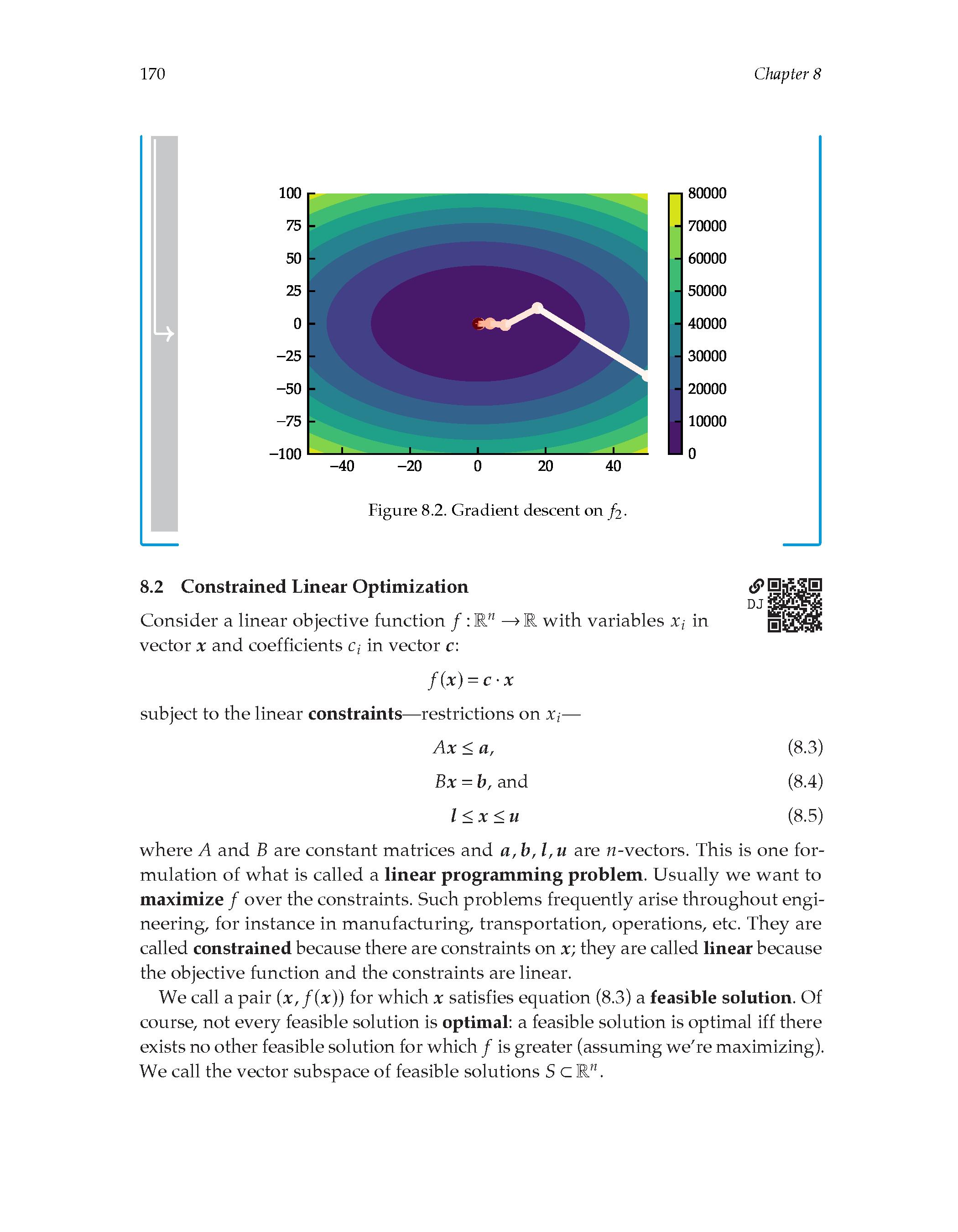
8.02 Constrained linear optimization
8.03 The simplex algorithm
8.04 Problems
9.01 Nonlinear state.space models
9.02 Nonlinear system characteristics
9.03 Simulating Nonlinear Systems
9.04 Problems
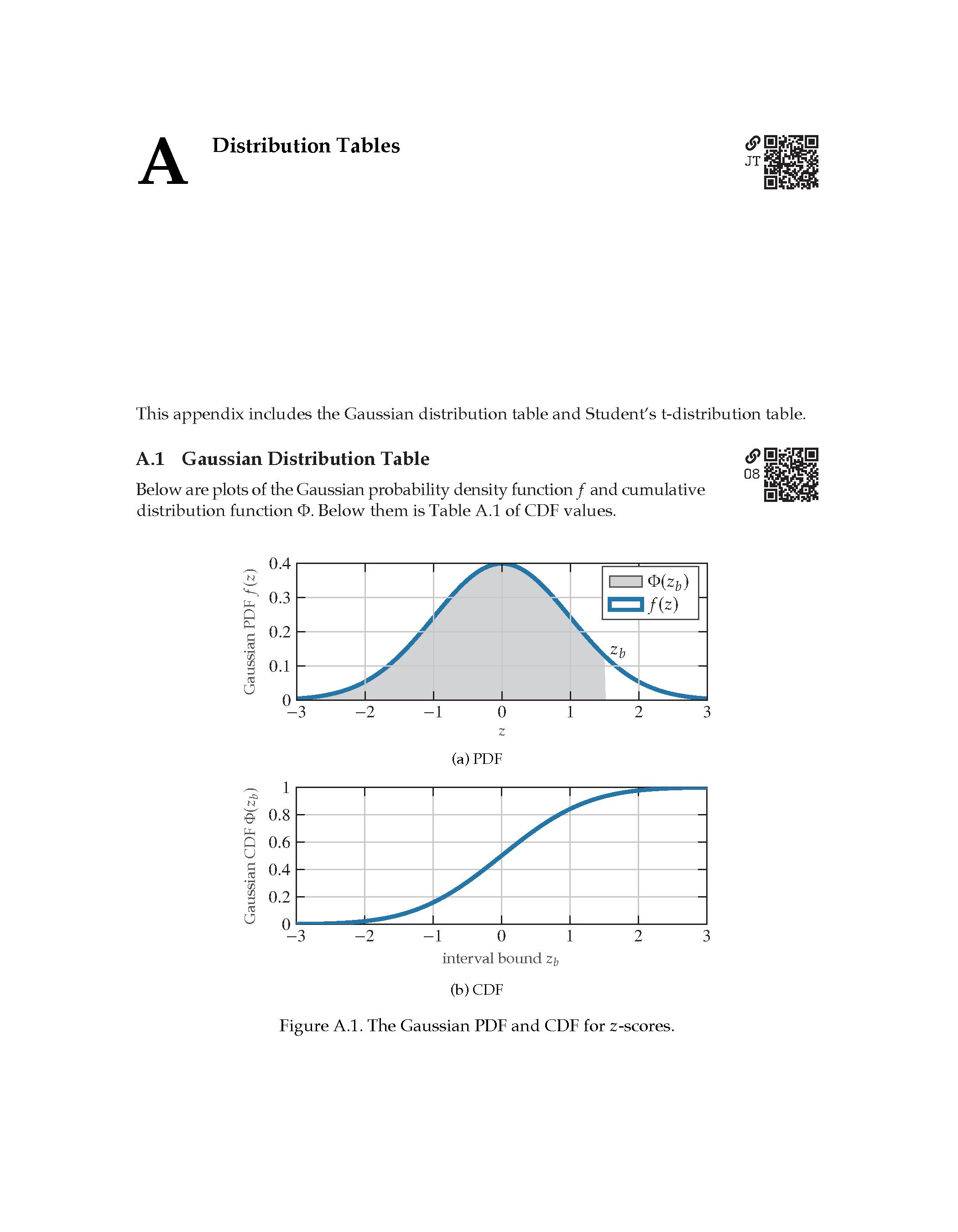
.01 Gaussian Distribution Table
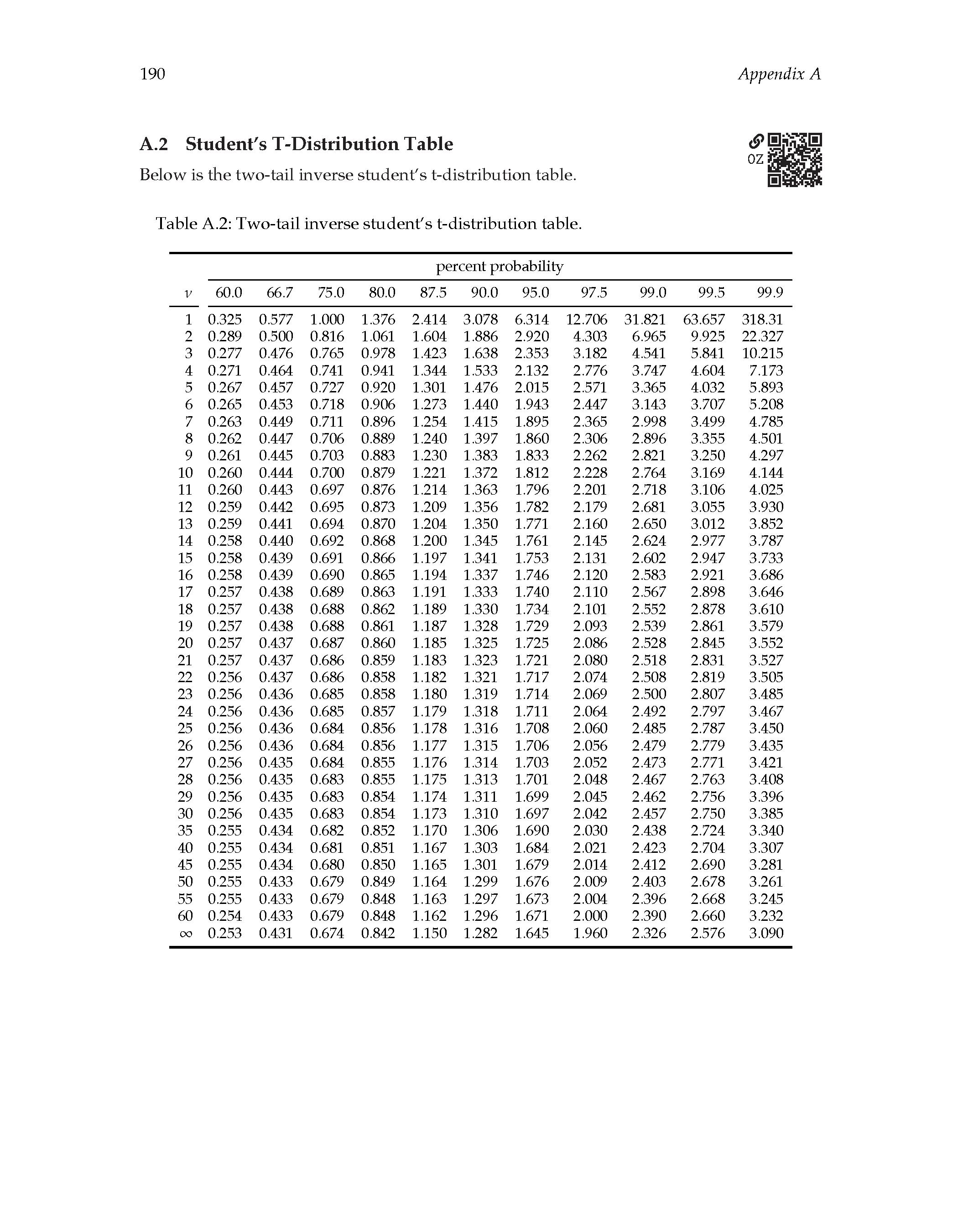
.02 Student s t.distribution Table
.01 Laplace Transforms
.02 Fourier Transforms
.01 Quadratic Forms
.02 Trigonometry
.03 Matrix Inverses
.04 Euler s Formulas
.05 Laplace Transforms